Bayes' Behavior

There is a concept in probability called Bayesian updating[1] that I think about quite a bit. I will skip all the math because while the equation is clear, the assumptions are incredibly subjective and make the equation worthless for this discussion. If you want a more detailed mathematical explanation, this guy seems good.
If you are familiar with the subject, you will notice that my use of this example is not "technically correct," but it is useful.
The idea of Bayesian updating is that you go into every experience with a prior belief about whether something may be true or not or whether something may happen or not. This value represents the culmination of all your previous experience and knowledge, representing your best estimate of what the world is like. Then, when you experience something new, that experience gets integrated into your belief system. Let's walk through an example.
Imagine you are going to visit the Ritz Carlton in Philadelphia for the first time. You have heard the experience is luxurious from advertisements, friends' opinions, and people on Reddit. Some of their comments were positive, some neutral, and some negative.
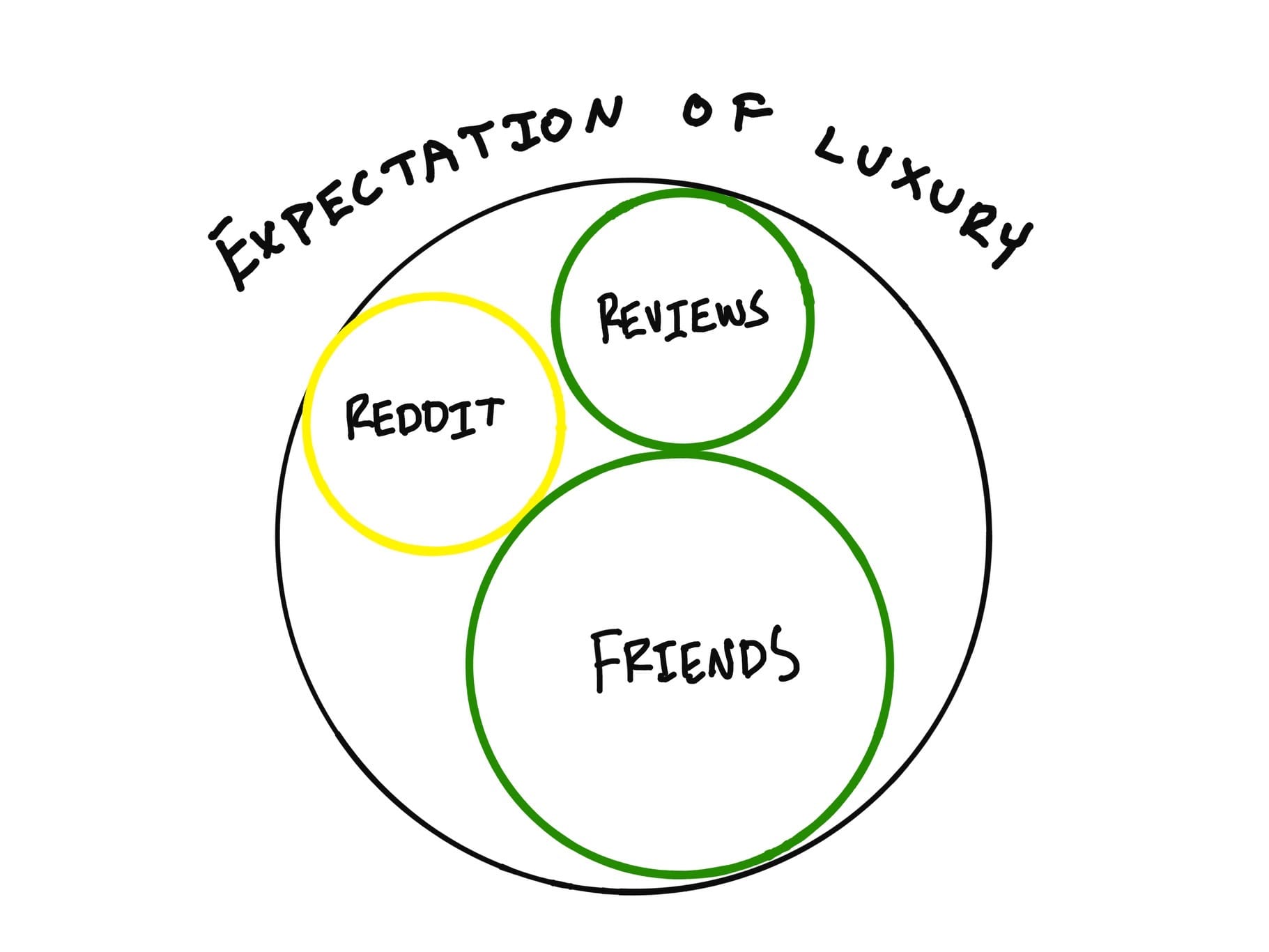
Ultimately, you had an incredible time and broadly incorporated that into your view of the Ritz.
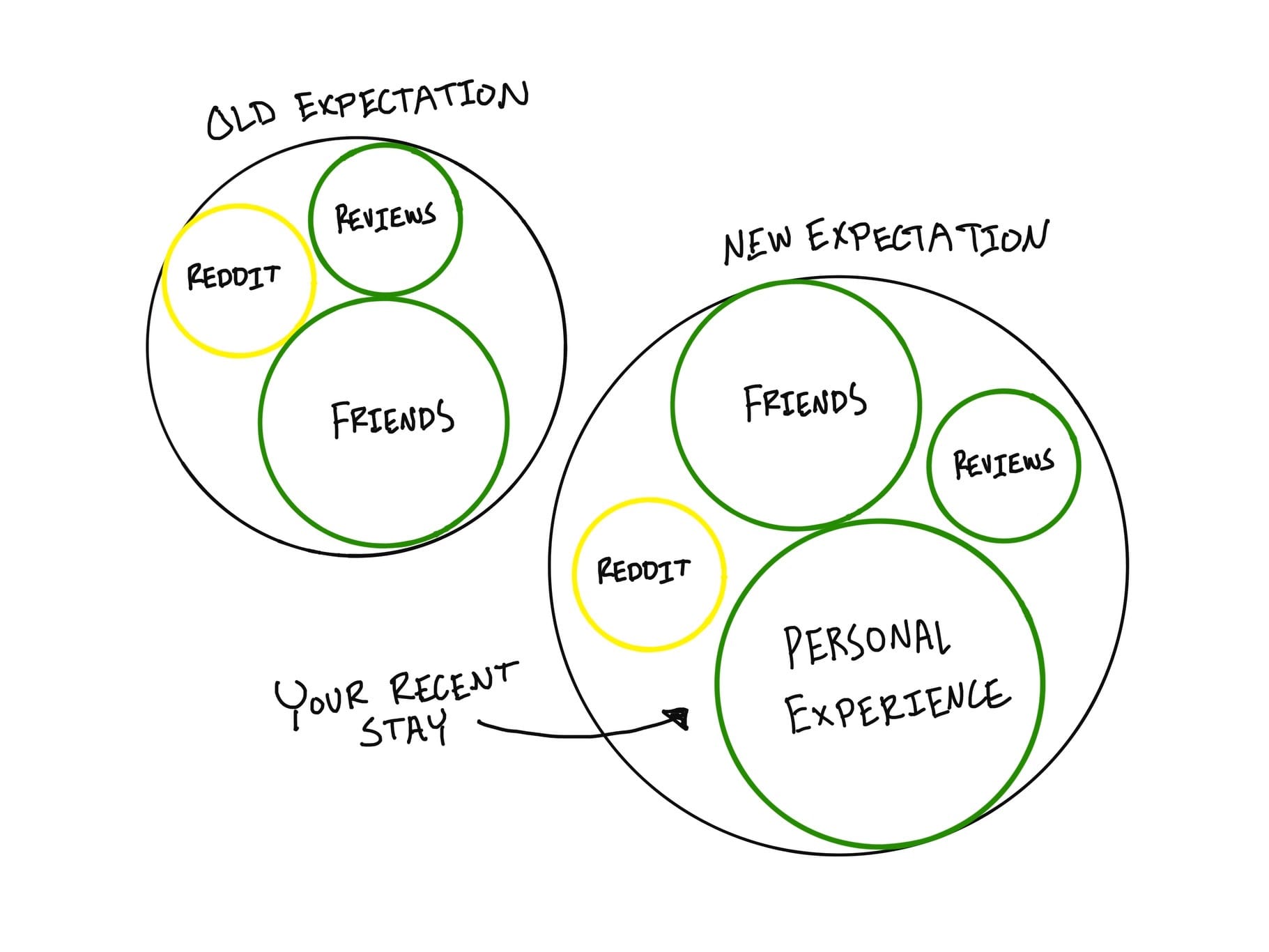
Notice how important personal experience is to you. In this case, your lived experience is more important than some comments on Reddit and understandably gets more weight.
Let’s jump forward. Twenty years later, you have stayed at Ritz properties (through some form of independent wealth?) every time you have traveled. You have amassed such experience that some would call you an expert.
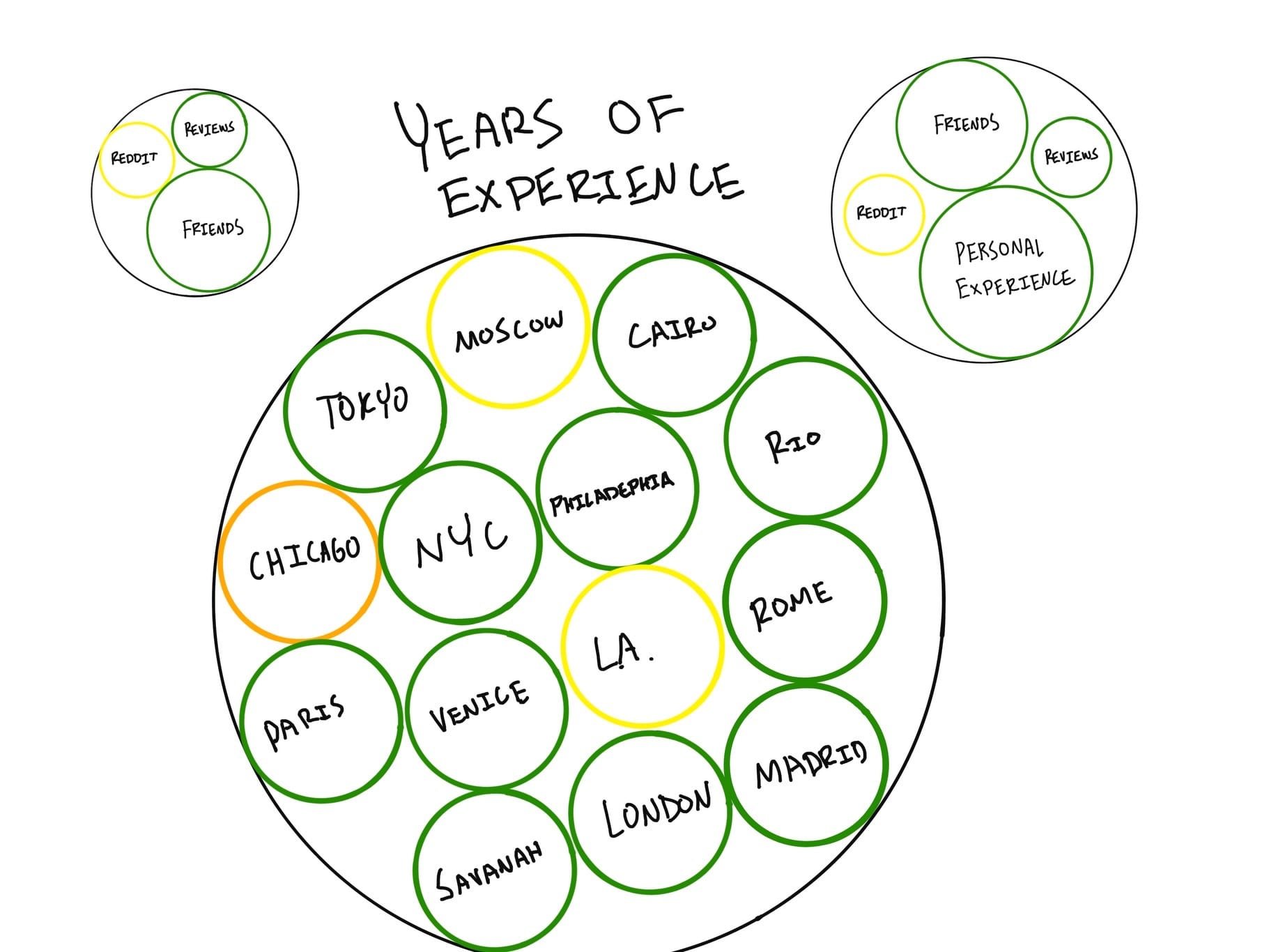
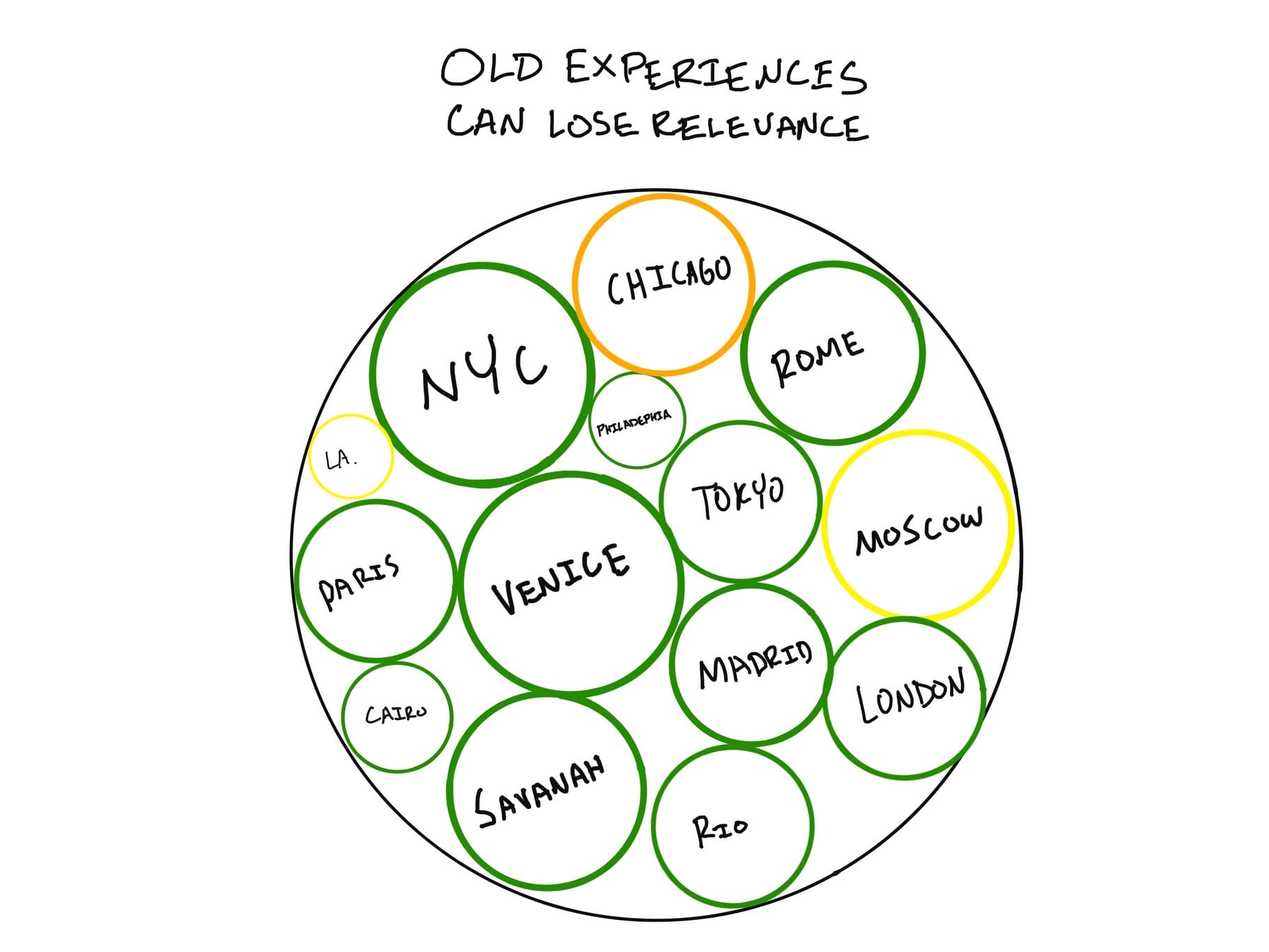
You end up in Philadelphia again and decide to stay at the Ritz, the same one you stayed at 20 years prior and haven't visited since. You're excited about the stay but find the bellhop slow and the concierge an unhelpful chatbot. Things have changed. We can't rely on our old experiences to always predict future events perfectly. The value of our experience decays over time unless it is refreshed.
Similar to this example with the Ritz, we constantly form opinions about things based on experiences and new information. What are the active things we must consider to make this realization helpful in crafting better opinions?
The Theorem's Assumptions
How experienced are you in a subject? The more you know about something, the harder it will be to influence you. If you have been to the Ritz 500 times, but your most recent experience was bad, you are less likely to believe it isn't all that is chalked up to be than if your first stay was bad.
How relevant is this information to what I am trying to evaluate? The bellhop may have been slow because the lobby was packed, and everyone arrived simultaneously for the event you were attending. That doesn't seem like something to be upset with the hotel about, and it shouldn't call their luxury status into doubt. On the other hand, replacing the concierge with a chatbot seems significant. The Ritz prides itself on their customer service, so this decision signifies a more substantial change. Note that this question ties into the first. How would you know what is important or not if you don’t possess experience?
How fast should I devalue old information or experiences? It depends on the subject. If you are talking about AI, progress is being made so quickly that what you learned last week could be outdated. On the other hand, human psychology hasn't changed much in hundreds of years, probably thousands. If you devalue things too quickly, you will be susceptible to recency bias, but if you devalue them too slowly, you may be too slow to adapt.
These questions fit into my images:
- Experience maps to the size of the encompassing circle.
- Information relevance maps to the sizes of the sub-thoughts inside the larger circle.
- The decay of information value is captured by the sub-thoughts shrinking over time.
Useful for understanding...
Bubbles - The internet becomes popular, nobody has significant experience in the domain, and over-optimism takes hold before people have run into enough walls to understand the practical limitations. Thus, the only sub-thought is limitless, and its assets get priced through the roof. This is a different play on a circle of competence. In this case, if your circle is not big enough (you don't have enough experience or knowledge on a subject), it is best not to play, or else you will get swept away by hysteria.
Science - Without concepts like Bayesian updating, science may never converge around a particular idea. Scientists disagree about various things at any given point, but over time, they all agree because enough experiments in different conditions can be run to justify conclusions. I won't delve much into it, but Covid was an excellent example of people with necessarily little experience, given how young the disease was making very definitive claims before enough experiments had been conducted.
News - I am generally anti-news for the reasons described above. If you want to learn about design, should you read design news daily, read classic books, or talk to professional designers? It depends on your goals, but the latter two are clear answers if you are trying to build a substantial depth of knowledge. I will counter that there is merit to following an industry over a long period, which is beneficial since you can feel the peaks and valleys that books can't provide.
Relationships - If someone repeatedly treats you poorly but later apologizes, the apology is out of character, not the poor treatment. People can change, but it sure seems to take a while. I would be biased to assume they haven't changed.
In the book Thinking in Systems, Donella Meadows says that “beguiling events” are one reason we misunderstand complex systems. Rather than focusing on a pattern of behavior, we get too caught up in a single experience, example, or data point. Coming into an opinion with a strong foundation, understanding how information in a domain shifts over time, and updating your beliefs as needed should help limit confusion and get you to a better understanding of the world around you.
- It has many names. Also known as Bayes' Theorem or Bayesian Inference.



